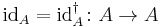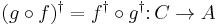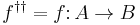Dagger category

In mathematics, a dagger category (also called involutive category or category with involution ^[1]^[2]) is a category equipped with a certain structure called dagger or involution. The name dagger category was coined by Selinger^[3].

1 Formal definition
2 Examples
3 Remarkable morphisms
4 See also
5 References

Formal definition

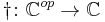A dagger category is a category $\mathbb{C}$ equipped with an involutive, identity-on-object functor $\dagger\colon \mathbb{C}^{op}\rightarrow\mathbb{C}$ .

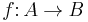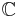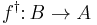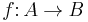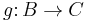In detail, this means that it associates to every morphism $f\colon A\to B$ in $\mathbb{C}$ its adjoint $f^\dagger\colon B\to A$ such that for all $f\colon A\to B$ and $g\colon B\to C$ ,

$\mathrm{id}_A=\mathrm{id}_A^\dagger\colon A\rightarrow A$
$(g\circ f)^\dagger=f^\dagger\circ g^\dagger\colon C\rightarrow A$
$f^{\dagger\dagger}=f\colon A\rightarrow B\,$

Note that in the previous definition, the term adjoint is used in the linear-algebraic sense, not in the category theoretic sense.

Some reputable sources ^[4] additionally require for a category with involution that its set of morphisms is partially ordered and that the order of morphisms is compatible with the composition of morphisms, that is a<b implies 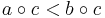$a\circ c<b\circ c$ for morphisms a, b, c whenever their sources and targets are compatible.

Examples

The category Rel of sets and relations possesses a dagger structure i.e. for a given relation 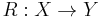$R:X\rightarrow Y$ in Rel, the relation 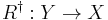$R^\dagger:Y\rightarrow X$ is the relational converse of $R$ .

A self-adjoint morphism is a symmetric relation.

The category FdHilb of finite dimensional Hilbert spaces also possesses a dagger structure: Given a linear map 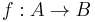$f:A\rightarrow B$ , the map 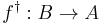$f^\dagger:B\rightarrow A$ is just its adjoint in the usual sense.

Remarkable morphisms

In a dagger category 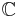$\mathbb{C}$ , a morphism $f$ is called

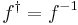unitary if $f^\dagger=f^{-1}$ ;
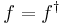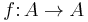self-adjoint if $f=f^\dagger$ (this is only possible for an endomorphism $f\colon A \to A$ ).

The terms unitary and self-adjoint in the previous definition are taken from the category of Hilbert spaces where the morphisms satisfying those properties are then unitary and self-adjoint in the usual sense.

References

^ M. Burgin, Categories with involution and correspondences in g-categories, IX All-Union Algebraic Colloquium, Gomel (1968), pp.34–35
^ J. Lambek, Diagram chasing in ordered categories with involution, Journal of Pure and Applied Algebra 143 (1999), No.1–3, 293–307
^ P. Selinger, Dagger compact closed categories and completely positive maps, Proceedings of the 3rd International Workshop on Quantum Programming Languages, Chicago, June 30–July 1, 2005.
^ Springer's Encyclopaedia of Mathematics. Category with involution

Dagger category

Contents

Formal definition

Examples

Remarkable morphisms

See also

References